Selon Daniel Kahneman, prix Nobel d’économie et auteur du livre  "Système 1 - Système 2" , notre cerveau fonctionne à deux vitesses :

Le système 1 est rapide, automatique, intuitif. Il intervient sans effort, en s’appuyant sur des impressions, des habitudes ou des émotions. C’est lui qui nous fait reconnaître une forme familière ou répondre sans réfléchir à « 2 + 2 ».

Le système 2, à l’inverse, est lent, réfléchi, logique. Il demande de l’attention, mobilise la mémoire de travail, et s’active lorsqu’on doit résoudre un problème complexe ou évaluer une situation nouvelle.

Nous avons besoin des deux pour penser efficacement. Dans un contexte d’apprentissage, il est crucial de savoir passer de l’un à l’autre : partir de l’intuition (Système 1), puis prendre du recul, analyser, et structurer sa pensée (Système 2).

Comment le conte et les mathématiques procèdent-ils au regard de ces deux systèmes de pensée ? 

On pourrait penser que le conte oral, par sa nature narrative et symbolique, mobilise avant tout le système 1 : 

• Il capte l’attention par l’émotion, les images, les rythmes.
• Il repose sur des structures familières : le héros, les épreuves, la répétition.
• Il emmène clairement l'auditeur dans un monde imaginaire, et se situe ainsi dans un registre d'attention proche de la rêverie. 

Cependant, bien vite, le héros doit mettre en place.... Son système 2 ! Sinon, il construira sa maison avec de la paille, parlera mal à la vieille femme qui détient pourtant des informations précieuses pour lui....les situations évoquées dans les contes, non seulement montrent l'importance d'une pensée raisonnée et construite, mais invitent l'auditeur à construire sa propre pensée logique.  Ainsi, "au fil du conte", le cerveau bascule  naturellement , presque sans y penser, vers le système 2. En cela, écouter un conte contribue à "préparer" l'activité mathématique. 

Celle-ci, pour sa part, s'inscrit clairement dans le système 2. Sauf que privée d'idée, d'intuition, d'esprit d'intiative, la recherche n'avance pas. Les mathématiques ont fondalementalement besoin de la dimension imaginaire et de l'intuition pour se développer. Et l'intuition, les représentations mentales, les analogies  qui ont lieu dans la recherche mathématique puisent leur source dans le système 1. 

En amenant les élèves à réfléchir sur les problèmes posés par le récit, c'est à dire en alliant sciemment le conte et les mathématiques, on invite les élèves, peut-être, à developper leur pensée analytique, leur logique et leur capacité d’abstraction sans pour autant étouffer la part un peu magique, intuitive et féconde, du système 1. 

Note : 

Le film de Matthew Brown, "L'home qui défiait l'infini" qui retrace la vie du mathématicien indien Srinivasa Ramanujan, illustre parfaitement, à mon sens, les deux modes de pensée décrits par Daniel Kahneman.

Ramanujan est l’archétype du penseur intuitif. Sans formation académique formelle, il découvre, invente, devine des formules mathématiques d’une beauté et d’une profondeur stupéfiantes, souvent sans démonstration. Il dit recevoir ses idées en rêve, ou comme des révélations. Sa pensée est fluide, spontanée, connectée à une intuition presque mystique des nombres.

 Il incarne donc le Système 1 : rapide, associatif, non verbal, mystérieusement fécond.

 G.H. Hardy incarne la tradition universitaire européenne, fondée sur la discipline du raisonnement. Il exige des démonstrations, il fonctionne par logique, structure, preuve, méthode. 

 Il est le représentant du Système 2 : lent, méthodique, critique, structurant.

 Le film montre la rencontre de ces deux hommes. Dans un premier temps ils se heurtent et s'opposent mais quand ils arrivent à travailler ensemble, chacun des deux apprend de l'autre et arrive à se dépasser

Ramanujan donne à Hardy accès à un monde d’idées et de formules qu’aucun esprit analytique pur n’aurait pu inventer seul. Hardy donne à ces idées la structure, la démonstration et la reconnaissance scientifique nécessaires pour qu’elles soient intégrées au corpus des mathématiques.

Le duo Ramanujan-Hardy symbolise ce que notre propre esprit peut accomplir lorsque nos deux systèmes — intuition (1) et raison (2) — coopèrent :

L’un imagine, explore L’autre vérifie et organise. Ensemble, ils ouvrent des portes que ni l’un ni l’autre ne pouvait franchir seul.

Le conte, comme l’intuition de Ramanujan, ouvre un espace imaginaire, fertile et symbolique. Les mathématiques, ou l'esprit scientifique en général, vient vérifier, puis structurer cette intuition. 

Comme Ramanujan et Hardy, dans un aller-retour entre inspiration et démonstration, entre système 1 et système 2, le conte et les mathématiques dialoguent. 

Projet Erasmus + "Myths et Maths"

Un projet international autour des contes et des mathématiques

Des contes et des mathématiques dans un projet Erasmus +

Journée de Formation autour du conte oral et des mathématiques aux Ateliers de la Rue Raisin à Saint Etienne. 

Le samedi 23 novembre 2024, j'aurai la joie d'animer aux côtés de Jean Porcherot, conteur et formateur aux Ateliers de la rue Raisin à Saint Etienne, une journée de pratiques et de réflexion  sur le thème "Contes et mathématiques". 

Voici le descriptif de cette journée: 

Samedi 23 novembre 2024

Journée de pratique et de réflexion animée par Laurence Chenou professeur de mathématiques et conteuse et Jean Porcherot conteur 9h30-16h30. Journée ouverte aux conteurs et aux enseignants non-conteurs, intéressés par cette nouvelle approche.

Donner du sens à la recherche est un enjeu fort pour l’apprentissage des mathématiques. Le conte merveilleux pourrait-il ouvrir une piste vers cet objectif ?  Allier le conte et les mathématiques peut aider l’enseignant à capter et à maintenir l’attention, à motiver les enfants à entrer dans l’aventure qu’est la résolution d’un problème, et à leur donner en même temps quelques clés langagières pour structurer leur pensée. A travers des mises en situation pratiques et des parties théoriques, le stage préparera enseignants et conteurs à monter et animer des projets autour du conte et des mathématiques. 

Infornations et inscriptions : 

Ateliers de la rue Raisin 16 rue Raisin 42000 Saint-Étienne

04 77 32 76 54 

rueraisin@gmail.com

Dans la pratique du conte oral, il arrive que l'on voie, chez un élève,  la parole "en construction": le jeune hésite, cherche ses mots, finalement les trouve, et peu à peu sa parole devient plus fluide. C'est toujours un moment précieux: à ce moment là, les autres écoutent toujours très attentivement, si intensément que le temps semble suspendu. 

A travers l'énigme des 12 soldats, on assiste cette fois à une autre construction: D'essai en essai, la pensée prend forme et s'élabore. Là aussi les élèves sont concentrés, attentifs à ce quefait l'autre et à ce que sa proposition apporte comme progrès. 

En image :

Merci à K. N, élève de 3eme,  pour cette énigme :

On dispose de neuf cubes, indiscernables au toucher.

8 sont en fer, le dernier est en plomb, (donc plus lourd).

Comment, avec exactement 2 pesées, trouver le cube de plomb ?   

Contes et Maths 2024, c'est parti !

Nouvel environnement, nouveau collège, nouveaux défis!

Deux classes de 6eme impliquées, et deux écoles primaires. 

Quand la fille du paysan veut bien épouser le prince, mais à la condition que pour le jour de leurs noces, il fasse défiler 12 soldats, rangés en 6 rangées de 4.....

Le mariage aura-t-il lieu ? 

Comment faire 4 triangles équilatéraux avec 6 craies ? 

Cette énigme est toujours pour moi un moment magique. Les élèvent tentent, cherchent, et surtout, chacun observe le raisonnement des autres. 

La solution est là:  

Les deux cyclistes et la mouche

Voici. 

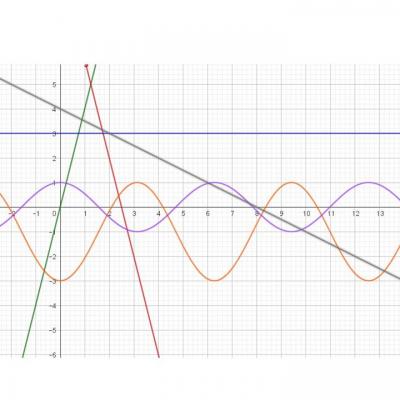
Deux villes A et B sont distantes de 100 Km

Un cycliste part de la ville A et va vers la ville B en roulant à la vitesse constante de 50 Km/h. Un deuxième cycliste part de la ville B et va vers la ville A en roulant lui aussi à 50km/h. 

Une mouche, qui pour sa part vole à 60 Km/h, va sans arrêt du nez du premier cycliste au nez du deuxième. 

Quand les deux cyclistes se rencontrent, combien de km aura fait la mouche ? 

C'est une belle reconnaissance de mon travail. 

"Pour faire des maths il faut savoir parler français". c'est une phrase de ma professeure de maths de terminale, Mme O. Boos, que je n'ai jamais oublié (comme je n'ai pas oublié non plus Jean Porcherot, mon professeur de Français du collège). Ils ont semé sur mon chemin des graines qui m'ont aidé à me construire et à surmonter les épreuves. 

En mathématiques la compétence "communiquer" a une part non négligeable, et on commence à s'apercevoir -  ou peut-être à mettre en pratique-  que la maitrise de la langue et la logique qui lui est inhérente y occupent une place centrale. L'épreuve du "Grand Oral" en mathématique a levé bien des problématiques. 

Je suis très fière de cet article. Je salue l'équipe des IREM qui m'a vraiment aidée à peaufiner et corriger mon style et la forme générale de mon propos, et tous ceux qui m'ont accompagnée dans ce cheminement. 

article-cle-en-main-revue-des-irem-oct-2023.pdf (390.94 Ko)

"Les mathématiques sont la poésie des sciences ", disait Léopold Sédar Senghor. 

Si les mathématiciens adhèrent en général à cette formule, il n'en n'est pas toujours de même pour les collégiens. Les motiver, leur donner le goût de l'effort et la volonté de chercher sont des challenges sans cesse à renouveller. 

Le conte oral a, parmi d'inombrables qualités, celles de captiver l'attention, d'enrichir le vocabulaire et la syntaxe, mais aussi de créer suffisament d'émotions pour que celui qui écoute puisse se projeter à la place du héros et souhaiter vivement son succès. Dans les projets que je propose, et que j'expose dans cet ouvrage, les adolescents sont amenés à entendre des histoires, mais aussi à résoudre des problèmes à la place du héros, avant des restituer les contes, les problèmes et leurs solutions, devant un public. 

Je mène ces projets en sixième depuis sept ans. A chaque fois je suis emerveillée par l'investissement des élèves, les petits miracles qui se produisent lorsqu'ils deviennent solidaire, travaillent ensemble et mettent leur talents personnels au service du groupe. 

Alors, n'hésitez plus, procurez vous ce livre ici : TheBookEdition

La Grande Oreille propose de découvrir les contes dans toute leur diversité (contes de tradition orale, mythes, légendes, contes urbains et contemporains, récits de vie…) et sous toutes leurs formes (spectacles de conteurs, conte comme outil d’éducation en milieu scolaire ou en bibliothèque, conte en milieu hospitalier…)

Un artile y a été consacré à mon manuel à l'automne 2021. Le voici :